Linux Cobbler自动部署装机
本文共 2721 字,大约阅读时间需要 9 分钟。
Cobbler自动部署装机
一、实验准备
- 一台Linux服务器(Centos7系统, IP:192.168.172.10)
- 一台空白虚拟机
- 需要连接上互联网,且虚拟机都使用NAT模式
- 相关软件包链接:https://pan.baidu.com/s/1lYbvL5106f7OJNK2Og9hzg 提取码:ndca
二、Cobbler自动装机服务搭建步骤
1.导入epel源
rpm –ivh epel-release-latest-7.noarch.rpm #安装依赖包yum list #自动加载在线更新源




2.安装Cobbler以及其相关服务软件包
yum install -y cobbler dhcp tftp-server pykickstart httpd rsync xinetd #各软件作用如下#cobbler 用来快速建立Linux网络安装环境#dhcp 用来为空白主机自动分配IP地址#tftp-server 提供引导镜像文件的下载#pykickstart 实现无人值守安装#httpd 作为控制台程序运行#rsync 实现数据同步#xinetd 提供访问控制、加强的日志和资源管理功能

3.修改cobbler主配置文件
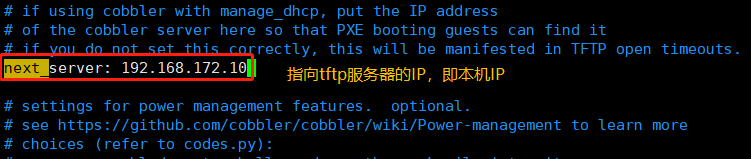
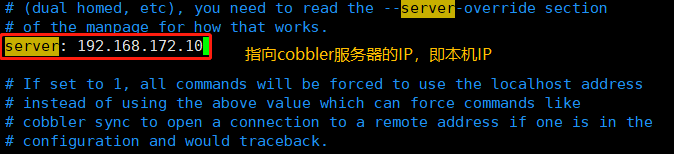
vim /etc/cobbler/settings#修改以下几项next_server: 192.168.172.10 #指向tftp服务器的IP,即本机IPserver: 192.168.172.10 #指向cobbler服务器的IP,即本机IPmanage_dhcp: 1 #让cobbler管理dhcp服务manage_rsync: 1 #让cobbler管理rsync服务manage_tftpd: 1 #让cobbler管理tftp服务



4.使用cobbler check 命令对Cobbler做检查设置,查询还需要更改配置的项目
cobbler check

5.开启tftp服务和rsync服务修改tftp的配置文件
修改tftp的配置文件vim /etc/xinetd.d/tftpdisable = no开启服务systemctl restart xinetd.servicesystemctl start rsyncd.service


6.下载引导操作系统文件
cobbler get-loaders

7.设置Cobbler用户初始密码
7.1使用盐值加密方式生成密钥
openssl passwd -1 -salt 'abc123' 'abc123' 任意字符可以随便写 安装完系统后root用户的密码为abc123

7.2将生成的密钥加入Cobbler配置文件中
vim /etc/cobbler/settings

8.配置dhcp服务
8.1修改Cobbler管理dhcp服务的模板文件
vim /etc/cobbler/dhcp.templatesubnet 192.168.80.0 netmask 255.255.255.0 { option routers 192.168.80.1; #修改网关 option domain-name-servers 192.168.80.2; #修改DNS,如果网卡使用的是dhcp模式,可通过nslookup 127.0.0.1 | grep server 查询DNS地址 option subnet-mask 255.255.255.0; range dynamic-bootp 192.168.80.100 192.168.80.200; #修改地址池 
8.2将配置好的模板文件同步到DHCP服务的配置文件中
cobbler sync

8.3重启DHCP服务
systemctl restart dhcpd.service

9.导入ISO镜像文件
9.1挂载镜像文件
mount /dev/sr0 /mnt

9.2导入iso镜像中的Linux 内核、初始化镜像文件
cobbler import --path=/mnt/ --name=CentOS-7-x86_64 --arch=x86_64#参数说明#--path 表示镜像所挂载的目录#--name 表示为安装源定义的名字#--atch 表示指定安装源的系统位数#默认导入存放路径为/var/www/cobbler/ks_mirror/CentOS-7-x86_64

9.3查看内核和初始化文件是否在在tftp-server 共享目录中
yum install -y tree #系统默认没有安装,需手动安装treetree /var/lib/tftpboot/images #查看文件是否存在


10.重启所有服务
systemctl restart cobblerd.servicesystemctl restart dhcpd.servicesystemctl restart xinetd.servicesystemctl restart httpd.service

11.再用cobbler check 对Cobbler做检查设置



12.所有配置完成后开启空白主机即可自动安装系统

 登陆成功
登陆成功 
三、安装左面系统
yum groupinstall "X Window System"yum update grub2-commonyum install -y grub2-efiyum install -y fwupdateyum install https://dl.fedoraproject.org/pub/epel/epel-release-latest-7.noarch.rpmyum groupinstall "GNOME Desktop"ln -sf /lib/systemd/system/runlevel5.target /etc/systemd/system/default.target ln -sf /lib/systemd/system/multi-user.target /etc/systemd/system/default.target ln -sf /lib/systemd/system/graphical.target /etc/systemd/system/default.target reboot

转载地址:http://wwag.baihongyu.com/
你可能感兴趣的文章
mysql源码安装
查看>>
Mysql源码安装过程中可能碰到的问题
查看>>
MySQL灵魂16问,你能撑到第几问?
查看>>
MySQL灵魂拷问:36题带你面试通关
查看>>
mysql状态分析之show global status
查看>>
mysql状态查看 QPS/TPS/缓存命中率查看
查看>>
mysql生成树形数据_mysql 实现树形的遍历
查看>>
mysql用于检索的关键字_Mysql全文搜索match...against的用法
查看>>
MySQL用得好好的,为什么要转ES?
查看>>
MySql用户以及权限的管理。
查看>>
MySQL用户权限配置:精细控制和远程访问的艺术!------文章最后有惊喜哦。
查看>>
mysql用户管理、常用语句、数据分备份恢复
查看>>
MySQL留疑问:left join时选on还是where?
查看>>
mysql登陆慢问题解决
查看>>
MySQL的 DDL和DML和DQL的基本语法
查看>>
mysql的 if else , case when then, IFNULL
查看>>
MySQL的10种常用数据类型
查看>>
MySQL的btree索引和hash索引的区别
查看>>
mysql的cast函数
查看>>
MySql的CRUD(增、删、改、查)操作
查看>>